Abstract

In order to split an idealized conical carrot into two pieces of equal volume, a cut should be made parallel to the base at approximately one fifth of the carrots total length measured up from the bottom. This simple rule of thumb warrants real world testing.

Motivation

It is of interest to cut a carrot into two pieces of equal volume. A trivial solution is to make a cut lengthwise from the tip to the base. However, this is often inconvenient because the carrot may be curved, longer than the knife’s blade, or both. Therefore, the cut shall be made across the shorter dimension.

Fully grown carrots generally taper significantly from one end to the other [citation needed]. In order to get a rough estimate for the position of the equal volume cut, an idealized model shall be adopted where the carrot is represented as a cone. It should be noted that by invoking Cavalieri’s Principle, the following derivation can reasonably be applied to mildly curved carrots [1].

Derivation

Consider an idealized conical carrot of length \( L \) and a circular base of radius \( r \) (Figure 1). The volume of this carrot is

$$\begin{equation}\label{V}\tag{1} V = \frac{1}{3}\pi r^2 L\ . \end{equation}$$

Figure 1. An idealized conical carrot. Original figure.

A fraction \( k \) will define where the cut should be made. The length of the base piece will be \( kL \) and the length of the tip piece will be \( L-kL \). The circle formed by the cut is defined to have a radius \( r_k \) (Figure 2).

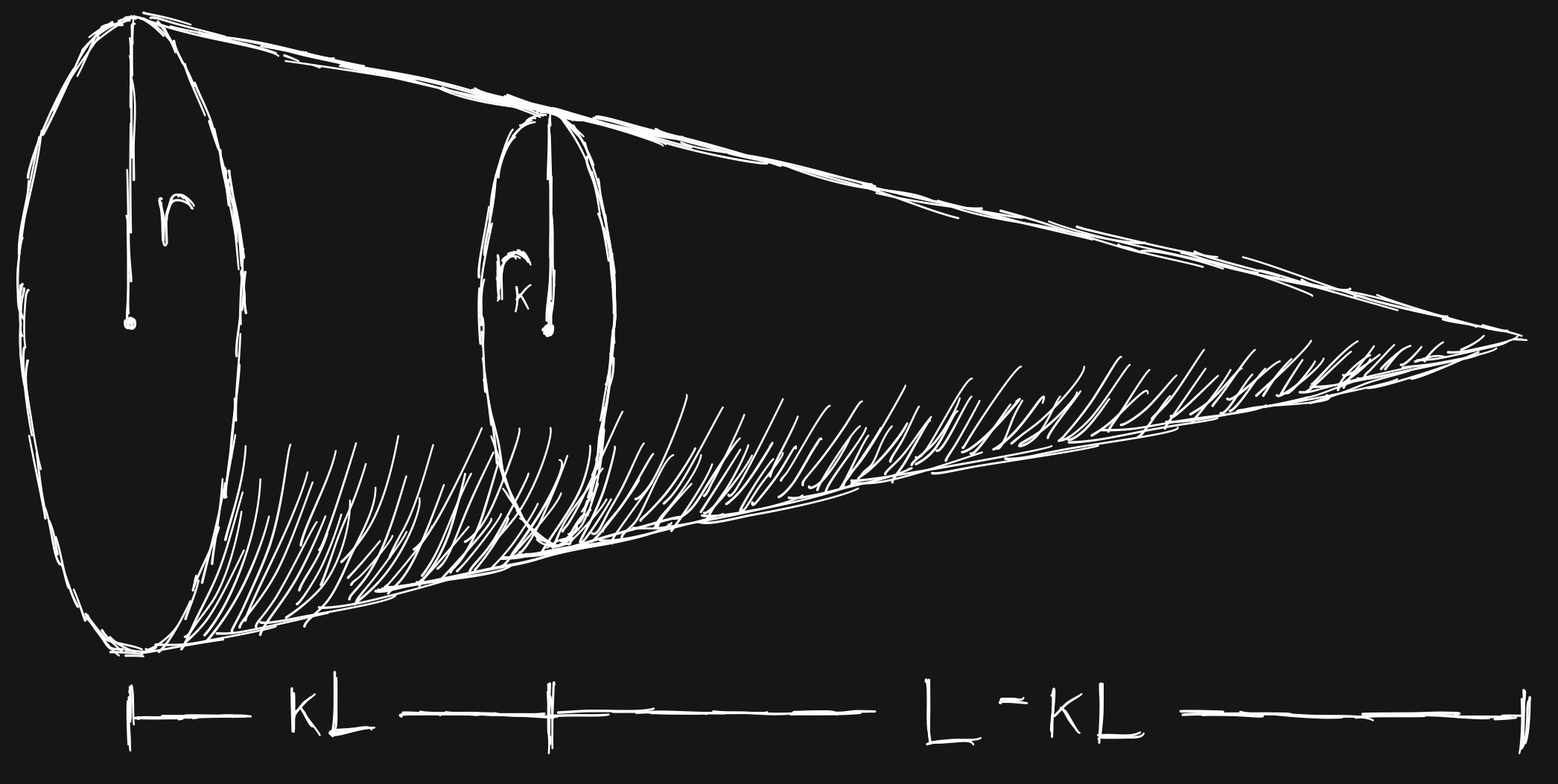Figure 2. The conical carrot with a cut a distance kL from the base. Original figure.

Since the cut is defined so the volumes of the base piece and the tip piece are equal, it is only necessary to find one of those volumes for this derivation. The tip piece is a cone and its volume is given by

$$\begin{equation}\label{tipVol}\tag{2} V_1 = \frac{1}{3}\pi r_k^2 (L-kL). \end{equation}$$

In order to find \( r_k \) in terms of \( r \) and \( k \), consider the two right triangles shown in Figure 3. The triangles were formed by drawing a line from the center of the base to the tip of the carrot. Because they share the angle \( \theta \), the trigonometric relation

$$\begin{equation}\label{bigT}\tag{3} \text{tan}(\theta) = \frac{r}{L} \end{equation}$$

can be defined for the big triangle and the similar relation

$$\begin{equation}\label{lilT}\tag{4} \text{tan}(\theta) = \frac{r_k}{L-kL} \end{equation}$$

can be defined for the smaller triangle.

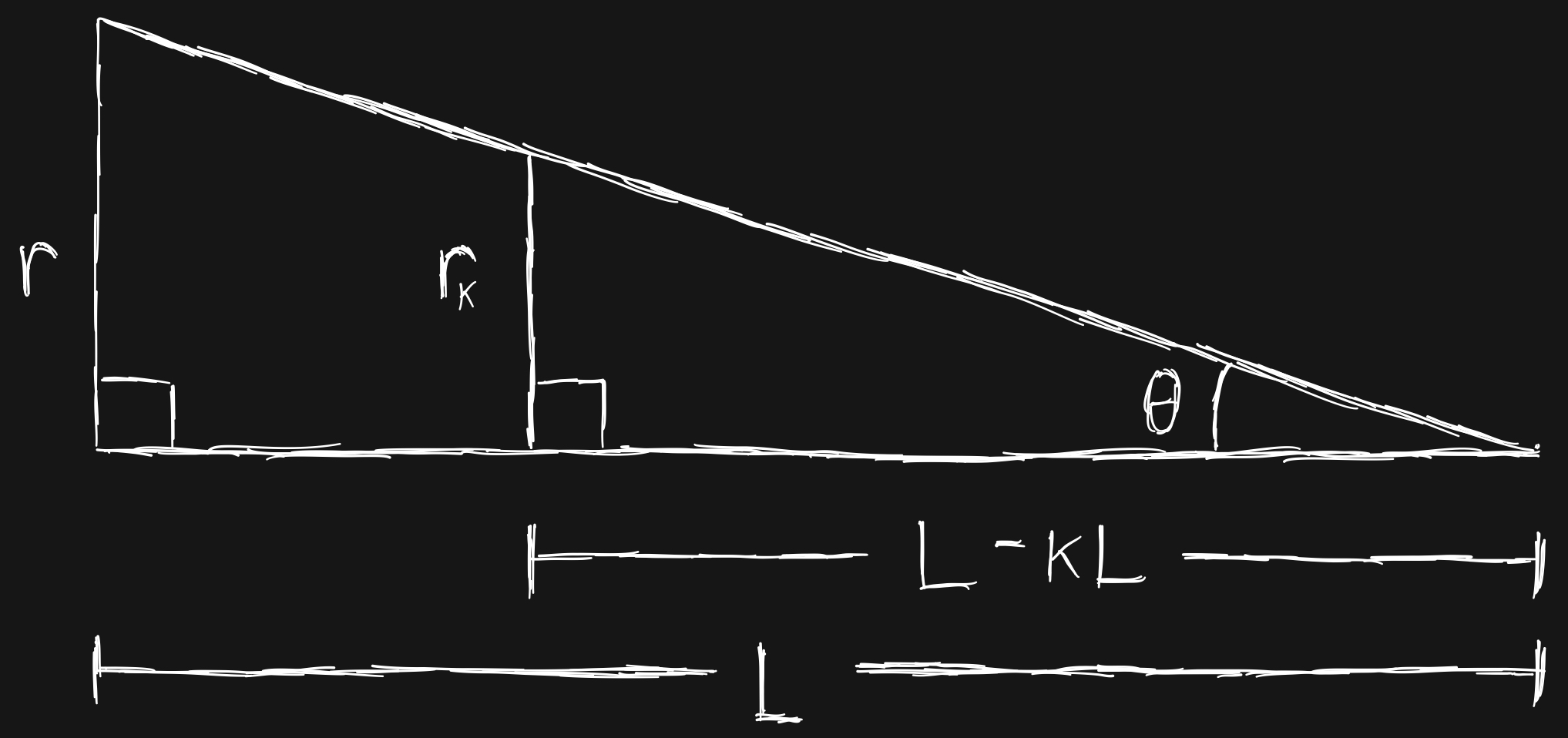Figure 3. Two right triangles formed by the full carrot and the tip piece. Original figure.

Setting equations \eqref{bigT} and \eqref{lilT} equal to each other allows for \( r_k \) to be found in terms of \( r \) and \( k \):

$$\begin{equation*} \frac{r_k}{L-kL} = \frac{r}{L} \end{equation*}$$ $$\begin{equation*} r_k = \frac{r}{L}(L-kL) \\ r_k = r(1-k) \end{equation*}$$

This may be substituted into equation \eqref{tipVol} for the volume of the tip \( V_1 \) to redefine the tip piece’s volume:

$$\begin{equation*} V_1 = \frac{1}{3}\pi [r(1-k)]^2 (L-kL) \\ V_1 = \frac{1}{3}\pi r^2 (1-k)^2 L(1-k) \\ \end{equation*}$$ $$\begin{equation} \label{tipVol2}\tag{5} V_1 = \frac{1}{3}\pi r^2 (1-k)^3 L \end{equation}$$

Because the tip and base pieces are of equal volume, the total volume \( V \) will be equal to twice the tip piece’s volume.

$$\begin{equation*} V = 2 V_1 \end{equation*}$$

Substituting the equations \eqref{V} and \eqref{tipVol2} into the above expression gives

$$\begin{equation*} \frac{1}{3}\pi r^2 L = 2\cdot \frac{1}{3}\pi r^2(1-k)^3 L. \end{equation*}$$

Canceling common factors from both sides leaves a relatively simple expression for \( k \).

$$\begin{equation*} 1 = 2(1-k)^3 \\ \left(\frac{1}{2}\right)^{1/3} = 1-k \\ k = 1 - \left(\frac{1}{2}\right)^{1/3} \end{equation*}$$

Evaluated numerically, \( k = 0.2063 \) which is reasonably close to a fifth.

$$\begin{equation*} \boxed{k \approx \frac{1}{5}} \end{equation*}$$

Conclusion

The equal volume cut of a conical carrot is approximately one fifth of the carrot’s total length from the base. This simple rule warrants testing, most likely using the water displacement method to measure the volume of real, irregularly shaped carrots.

References

[1] “Cavalier’s Principle.” Wikipedia, 7 November 2018. Web Link.